
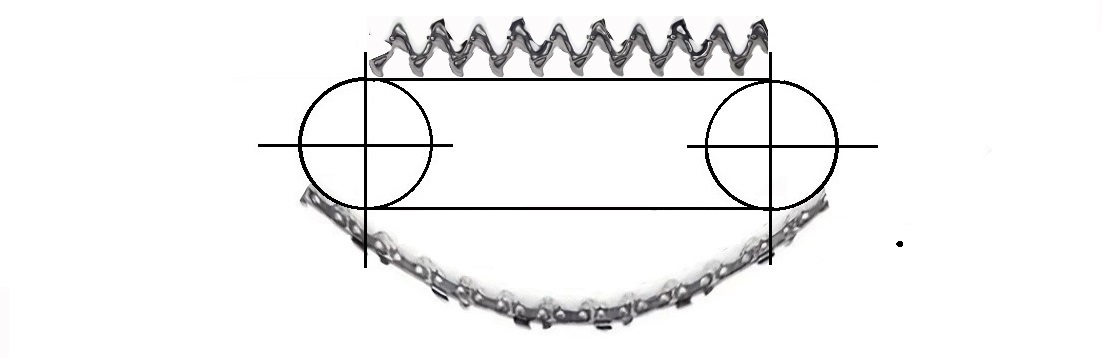
The chainsaw paradox is a thought experiment that does not occur in nature. No chain can move at anything close to c. It relates solely to the length contraction of the special theory of relativity. Everything beyond that is ignored. We ignore the time of acceleration and deceleration. It is undisputed that the chain breaks because it heats up and burns up due to the friction on the blade. However, that has nothing to do with length contraction. It is also undisputed that there are complications because the upper half of the chain is pushed and the lower half of the chain is pulled, although this does not require simultaneity. However, that has nothing to do with length contraction. Just as the chain breaks at the turning points due to acceleration, deceleration and centrifugal force. But that has nothing to do with length contraction either. To exclude irrelevant effects, the experiment only relates to the straight part of the chain while it moves evenly at approximately c. Since the chain contracts along its entire length, you can take any section. Let's take the straight section. In this section, neither the chain nor the sword can tell who is moving and who is at rest. The principle of relativity does not allow this. One could even relate only individual terms to the length contraction or only individual atoms of a term. - And simultaneity or the lack of simultaneity plays no role in the chainsaw paradox. Only one gear is driven. The second one runs freely.
Page 1 of 8

Both the chain and the sword are in the cutout between
the two axes of rotation in both systems either at
rest or in a uniform, straight-line movement at
approximately the speed of light. According to the
principle of relativity, there is no difference
between rest and uniform linear motion. Nothing in the
world can distinguish between these two states. The
thought experiment refers to a phase where the chain
has already reached its speed of approximately c and
is therefore moving uniformly in a straight line
across the middle part of the sword.
In the sword system the chain is shortened. The chain breaks.

In the chain system, the sword is shortened. The chain sags.
Reality only
knows one process. Either the chain breaks or it
sags? There are many perspectives, but there is
only one reality. What follows the 3-fold
contraction chaos? Does the chain break or does it
sag? Can a connected chain have 3 different
lengths? - Can 3 times pass at different speeds in
a connected chain? Reality does not depend on what
external observers observe. External observations
do not interfere with internal reality.
The length chaos
.
A buyer buys a chainsaw. The total length of the chain is 1 m. The total circumference of the bar is 2 m. The buyer asks the seller how the chain can fit on the bar? The seller replies: "The chain just has to move fast enough, because then the bar gets shorter for the chain and then it fits on the bar." - "Can you demonstrate it to me," asks the buyer? "Only if you have until tomorrow," says the seller, "because due to time dilation it takes about a day for the chain to fit on the bar."
The length chaos
.
A buyer buys a chainsaw. The total length of the chain is 1 m. The total circumference of the bar is 2 m. The buyer asks the seller how the chain can fit on the bar? The seller replies: "The chain just has to move fast enough, because then the bar gets shorter for the chain and then it fits on the bar." - "Can you demonstrate it to me," asks the buyer? "Only if you have until tomorrow," says the seller, "because due to time dilation it takes about a day for the chain to fit on the bar."
The lower
links in the chain say to the upper links in the
chain: “But you’re short compared to us.”
The upper links say to the lower links: “Strange,
but we were just about to say the same thing to
you.” Say the sword: “Quiet,
you short limbs.” - “Hello, what happened
to you? You are wider than you are long,”
say the limbs to the sword.
Page 2 of 8
Will the chain break
or sag? Either way, a chain tensioner will prevent
both and keep the chain on the bar. The position
of the chain tensioner is recorded in a measuring
device.
Situation 1) Both systems, the bar and the chain, are at rest relative to each other. The measuring device measures the position of the chain tensioner.
Situation 1) Both systems, the bar and the chain, are at rest relative to each other. The measuring device measures the position of the chain tensioner.
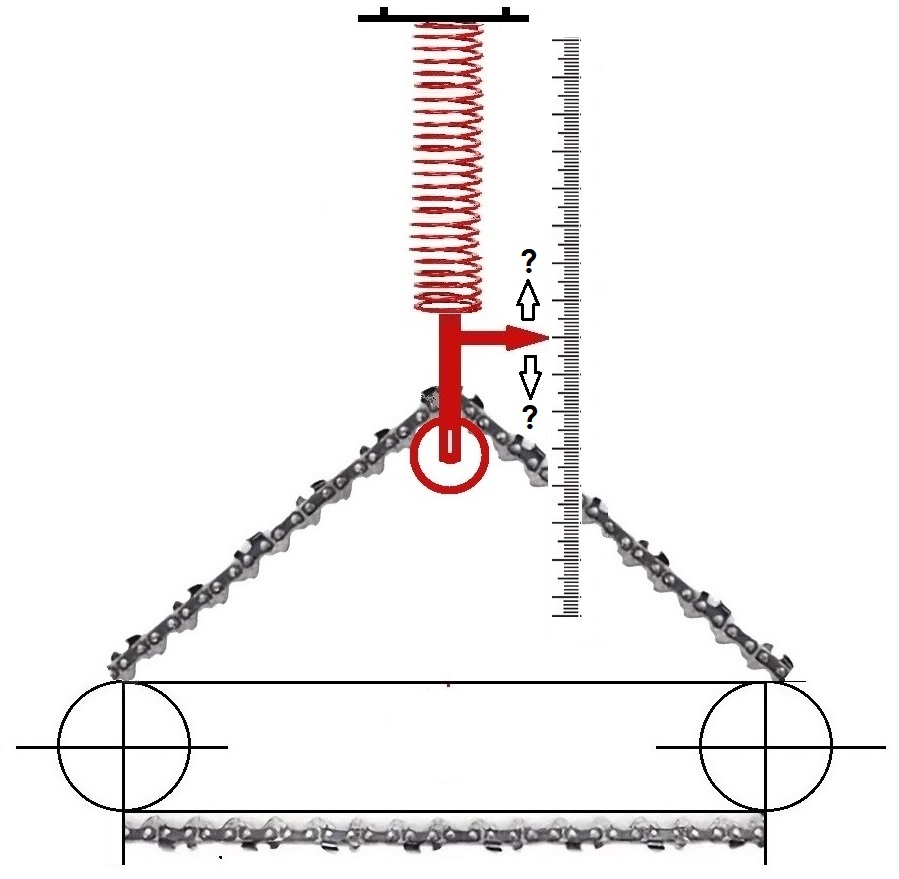
Situation 2) The chain
accelerates to 0.9 c and subsequently moves evenly
along the middle sections. The chain tensioner
keeps the chain taut and undamaged on the bar,
whatever effects occur in all systems.
System 1) Sword relative to the upper and lower chain.
System 2) Upper and lower chain relative to the sword.
System 3) Upper chain relative to the lower chain.
System 4) Lower chain relative to the upper chain.
Every system is at rest or
in uniform motion relative to all other systems.
The principle of relativity does not allow any
distinction. Inertial systems don't change
anything.
What value
do all systems read on the scale?
Mathematics answers this question. But is there a reality behind this answer?
Mathematics answers this question. But is there a reality behind this answer?
The chain tightener asks the
chain: “How does it feel to be 100%, 44%, and
10% long?” The chain says: “My length
is always 100%. What the others see doesn’t
concern me.” The chain tightener says to
the sword: “How does it feel to be 100% and
44% long?” The sword says: “My length
is always 100%. What the others see doesn’t
concern me.” The chain tightener then
says: “Okay, if everyone is the way they’ve
always been, then I’ll tighten the chain the
way I’ve always tightened it. Then I’ll always
show what I’ve always shown. What others read
on the scale does not concern me.” Being
is what matters, not appearances. The number of
chain links per section must be the same for
everyone involved.
Page 3 of 8
Special
relativity
Time dilation
The twin paradox
Time dilation
The twin paradox
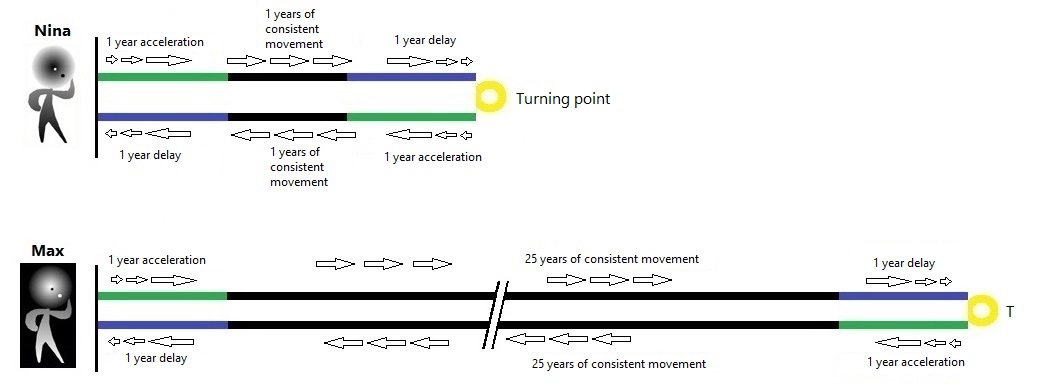
The
twins Nina and Max go on a journey. They both leave
at the same time from the same starting point and
move constantly under the same influence of gravity
during their journey. This means that there are no
different effects due to different gravity.
All subsequent actions occur according to their own time.
Neither looks at the other's clock!
Both accelerate for 1 year. After 1 year of acceleration, both have reached 0.9 c.
For both, the transition from acceleration to uniform motion is the same.
Nina moves uniformly for 1 year, then she decelerates for 1 year to the turning point and returns in the opposite direction. She rests there for 48 years until her brother arrives. Max moves uniformly for 25 years, then he decelerates for 1 year to the turning point and returns in the opposite direction.
Both have the same accelerations, decelerations, turning point and all related transitions according to their own clock. Nothing is different between the two. The only difference is that Max moves uniformly in a straight line for 48 years longer relative to Nina. According to the principle of relativity, during the 48 years neither of them can tell who is moving and who is at rest. The principle of relativity does not allow for any distinction, because uniform linear motion and rest are the same thing. Nothing in the world can tell the difference.
How old are the two 20-year-old twins when they meet again after a long time?
All subsequent actions occur according to their own time.
Neither looks at the other's clock!
Both accelerate for 1 year. After 1 year of acceleration, both have reached 0.9 c.
For both, the transition from acceleration to uniform motion is the same.
Nina moves uniformly for 1 year, then she decelerates for 1 year to the turning point and returns in the opposite direction. She rests there for 48 years until her brother arrives. Max moves uniformly for 25 years, then he decelerates for 1 year to the turning point and returns in the opposite direction.
Both have the same accelerations, decelerations, turning point and all related transitions according to their own clock. Nothing is different between the two. The only difference is that Max moves uniformly in a straight line for 48 years longer relative to Nina. According to the principle of relativity, during the 48 years neither of them can tell who is moving and who is at rest. The principle of relativity does not allow for any distinction, because uniform linear motion and rest are the same thing. Nothing in the world can tell the difference.
How old are the two 20-year-old twins when they meet again after a long time?
Page 4 of 8
The
following thought experiment is helpful in
visualizing the twin paradox: 2 pendulum clocks. You
set one up at home and the other on a carousel. When
the carousel starts to turn, the pendulum clock
changes to a stronger field of force. In this case,
due to centrifugal force. The stronger the field of
force, the slower the pendulum swings. The clock
runs slower accordingly. The same applies to the
field of force of acceleration, deceleration or
gravity. However, this has nothing to do with the
time dilation of the special theory of relativity.
This is an effect of the general theory of
relativity and does not interfere with the time
dilation of the special theory of relativity. If the
pendulum clock leaves the stronger field of force,
the pendulum swings just as quickly as before. She
can't make up for the lost time afterwards. From the
timing behavior, you can tell whether a clock has
changed its field of force (gravity, acceleration,
deceleration, centrifugal force). From the timing
behavior, you cannot tell whether a clock is at rest
or moving uniformly in a straight line. The
principle of relativity does not differentiate
between rest and movement. In both cases, the clock
runs at the same rate. Clocks at rest and clocks
moving in a straight line at the same speed in the
same force field run at the same speed. They run at
the same rate.
When it was first developed, Hendrik Lorentz related the Lorentz factor to electromagnetism. In order to explain the constant speed of light without ether, it was only later mathematically interpreted into space and time.
When it was first developed, Hendrik Lorentz related the Lorentz factor to electromagnetism. In order to explain the constant speed of light without ether, it was only later mathematically interpreted into space and time.
Mathematics
There is a real mathematics behind every reality.
That is undisputed. No one has ever observed
anything else. If there had been a God who created
everything, he would have been a mathematician,
because every reality is related to mathematics. The
reverse is not the case, however. There is not
necessarily a reality behind every mathematical
result. There is very often a reality behind it, in
fact almost always, but not always.
If a farmer harvests 1 ton of potatoes in 1 year, then he will harvest 300 tons of potatoes in 300 years. The mathematics is correct. Any mathematician can confirm that. 1 x 300 = 300
But there is no reality behind it, because no farmer lives for 300 years. If I pour 1 liter of water into a jug, then mathematically speaking I have 1 liter of water in the jug. In reality, however, I only have about 1 liter of water in the jug.
If a farmer harvests 1 ton of potatoes in 1 year, then he will harvest 300 tons of potatoes in 300 years. The mathematics is correct. Any mathematician can confirm that. 1 x 300 = 300
But there is no reality behind it, because no farmer lives for 300 years. If I pour 1 liter of water into a jug, then mathematically speaking I have 1 liter of water in the jug. In reality, however, I only have about 1 liter of water in the jug.

Page 5 of 8
Relativistic mass and momentum
The equivalence principle:
Inertial and gravitational mass are equivalent.
Newton and Einstein


Impressum: badhofer Steyr AUSTRIA badhofer.com
admin@badhofer.com 22.05 2024 updated: 14.11.2024
 Printversion:
paradox.pdf
Printversion:
paradox.pdf
Relativistic mass and momentum
The equivalence principle:
Inertial and gravitational mass are equivalent.
At some point, the values of inertial and
gravitational mass were related in such a way that
they add up to 1:1 here on our planet. In everyday
language, this means: 1 kg inertial mass = 1 kg
gravitational mass. This is an arbitrary
assumption that has proven itself here on our
planet. The values could just as well have been
set at 1:10. This means: 1 kg inertial mass = 10
kg gravitational mass. The equivalence of inertial
and gravitational mass would not have
changed.
Suppose I weigh 60 kg here on earth. This means I have 60 kg of inertial mass and 60 kg of gravitational mass. If I were to eat twice my weight, I would have 120 kg of inertial mass and 120 kg of gravitational mass. If I fly to the moon with my 60 kg weight, I will have 10 kg of gravitational mass there due to the reduced gravity and still 60 kg of inertial mass. If I double my weight on the moon by eating, I would have 20 kg of gravitational mass and 120 kg of inert mass. Because 2x10 = 20 and 2x60 = 120. If I fly to the ISS with my 60 kg, I would have 0 kg of gravitational mass and 60 kg of inert mass in zero gravity. If I eat myself up to twice that weight, I would have 0 kg of gravitational mass and 120 kg of inert mass. Because 2x0 = 0 and 2x60 = 120
The momentum depends on the inertial mass and the speed. The inertia of a mass depends on the number of atoms and their weight. If the number of atoms in a mass does not change and the weight of the atoms does not change because the components of the atoms change, then the inertial mass remains the same throughout the universe. It does not matter whether you move it evenly in a straight line, accelerate it, decelerate it, rotate it in a circle, etc. The inertial mass always remains the same. It never changes. Mass and energy are equivalent. A relativistic increase in mass would also be a relativistic increase in energy. How does a relativistic increase in energy relate to the conservation of energy?
If there is a relativistic, uniform speed in a straight line, then there must also be a relativistic acceleration. Because when a relativistic, uniform motion in a straight line begins to accelerate, then it also accelerates relativistically. Acceleration and gravity are equal. Nothing in the world can distinguish between acceleration and gravity. If there is a relativistic acceleration, then there must also be a relativistic gravity. Because there would only be a relativistic acceleration, but no relativistic gravity, it would make a difference whether an object accelerates or whether it is in the sphere of influence of gravity. Regardless of external measurability. Reality does not depend on whether it is measurable or not. What is relativistic gravity?
Everything has to do with energy. What is a relativistic energy? How does a relativistic energy relate to the conservation of energy?
Page 6 of 8Suppose I weigh 60 kg here on earth. This means I have 60 kg of inertial mass and 60 kg of gravitational mass. If I were to eat twice my weight, I would have 120 kg of inertial mass and 120 kg of gravitational mass. If I fly to the moon with my 60 kg weight, I will have 10 kg of gravitational mass there due to the reduced gravity and still 60 kg of inertial mass. If I double my weight on the moon by eating, I would have 20 kg of gravitational mass and 120 kg of inert mass. Because 2x10 = 20 and 2x60 = 120. If I fly to the ISS with my 60 kg, I would have 0 kg of gravitational mass and 60 kg of inert mass in zero gravity. If I eat myself up to twice that weight, I would have 0 kg of gravitational mass and 120 kg of inert mass. Because 2x0 = 0 and 2x60 = 120
The momentum depends on the inertial mass and the speed. The inertia of a mass depends on the number of atoms and their weight. If the number of atoms in a mass does not change and the weight of the atoms does not change because the components of the atoms change, then the inertial mass remains the same throughout the universe. It does not matter whether you move it evenly in a straight line, accelerate it, decelerate it, rotate it in a circle, etc. The inertial mass always remains the same. It never changes. Mass and energy are equivalent. A relativistic increase in mass would also be a relativistic increase in energy. How does a relativistic increase in energy relate to the conservation of energy?
If there is a relativistic, uniform speed in a straight line, then there must also be a relativistic acceleration. Because when a relativistic, uniform motion in a straight line begins to accelerate, then it also accelerates relativistically. Acceleration and gravity are equal. Nothing in the world can distinguish between acceleration and gravity. If there is a relativistic acceleration, then there must also be a relativistic gravity. Because there would only be a relativistic acceleration, but no relativistic gravity, it would make a difference whether an object accelerates or whether it is in the sphere of influence of gravity. Regardless of external measurability. Reality does not depend on whether it is measurable or not. What is relativistic gravity?
Everything has to do with energy. What is a relativistic energy? How does a relativistic energy relate to the conservation of energy?
Newton and Einstein

Newton and Einstein
sit on a bench in the forest. Einstein says to
Newton: "I see a black
rocket that weighs 1 g and flies uniformly
and straight over my head at 0.9 c
relative to me." Newton
then says: "I see a white rocket that
weighs 1 g and flies uniformly and straight
over my head at 0.9 c relative to
me." You know, I think they're going to
collide over our heads. Should we take
cover?"
Page 7 of 8

Newton and Einstein
calculate the momentum that is decisive in
the central elastic collision of the rockets
in order to know who needs to take cover
more. What value do they both calculate for
the respective momentum of each rocket?
Page 7 of 8
Variant 2 Both
rockets are moving towards each other at
0.99 c relative to Newton and
Einstein. With what momentum do the two
rockets collide? Does each rocket only
feel its own momentum or does each
rocket feel its share of the
relativistic total momentum of the two
rockets relative to each other?
|
Variant 3 Before
they collide, the two 1 g
rockets hit a 1 g ball that is
at rest relative to Newton and Einstein
in the middle of its trajectory. With
what momentum do the rockets hit the
ball? The ball remains at rest.
|
Variant 4 The
ball does not weigh 1 g, but 2
g. It
is twice as heavy as in variant 3. The
rockets always hit the ball at the same
time (relative to the ball). How do both
rockets recognize when they collide
whether they are in variant 1, 2 or 3?
|
Variant
5) In this variant, both rockets have
a speed of 0.99 c


Before they collide, the
two 1 g rockets each hit a 2 g ball, which is
at rest relative to each other and relative to
Newton and Einstein in the middle of its
trajectory. Both rockets give part of their
momentum to the respective ball. With what
momentum do the two 2 g balls collide?
Which value does Newton calculate and which value does Einstein calculate? All of the participants are either at rest or moving uniformly in a straight line relative to one another. There is no difference between being at rest and moving uniformly in a straight line. The principle of relativity does not allow for a distinction. - Who needs to take cover more when something crashes above them? Newton or Einstein? There are many perspectives, but only one reality! Behind every reality there is correct mathematics. But the reverse is not true. Behind every correct mathematics there is not necessarily a reality! Which real impulses do both calculate? In a collision it is irrelevant whether the impulse was created by a classical or a relativistic speed. Impulse = impulse. The impulse already contains the criteria for its creation.
All clear: Issac and Albert are safe!
In classic central elastic collisions, the original momentum is conserved throughout the entire action. The conservation of momentum applies to both Newton and Einstein.
Which value does Newton calculate and which value does Einstein calculate? All of the participants are either at rest or moving uniformly in a straight line relative to one another. There is no difference between being at rest and moving uniformly in a straight line. The principle of relativity does not allow for a distinction. - Who needs to take cover more when something crashes above them? Newton or Einstein? There are many perspectives, but only one reality! Behind every reality there is correct mathematics. But the reverse is not true. Behind every correct mathematics there is not necessarily a reality! Which real impulses do both calculate? In a collision it is irrelevant whether the impulse was created by a classical or a relativistic speed. Impulse = impulse. The impulse already contains the criteria for its creation.
All clear: Issac and Albert are safe!
In classic central elastic collisions, the original momentum is conserved throughout the entire action. The conservation of momentum applies to both Newton and Einstein.
Impressum: badhofer Steyr AUSTRIA badhofer.com
admin@badhofer.com 22.05 2024 updated: 14.11.2024
 Printversion:
paradox.pdf
Printversion:
paradox.pdfPage 8 of 8